Analyse comparative des modèles champs de phase pour la simulation de la propagation de fissure en milieux anisotropes

MEALOR Days

F. Loiseau
flavien.loiseau@ensta-paris.fr

IMSIA, ENSTA Paris, CNRS, EDF, Institut Polytechnique de Paris 91120 Palaiseau, France

V. Lazarus
veronique.lazarus@ensta-paris.fr

November 7, 2024

Fracture in 3D-printed structures

Duplex stainless steel by DED (Roucou et al., 2023)

Polycarbonate CT specimen by FDM (Zhai, 2023)

Global objective

Modelling and simulating crack propagation in 3D-printed structures

Fracture mechanics problem

We consider

  • a domain \(\Omega\) with a pre-crack \(\Gamma_0\),
  • an elastic material (\(E\), \(\nu\)),
  • a force or displacement load,

and we want to determine

  • the crack-path,
  • the force-displacement curve,
  • the evolution of the displacement field.

To solve this problem, we want to employ numerical methods.

Accounting for fracture anisotropy

Generalization of the Maximum Energy Release Rate (GMERR)

The crack propagates when:

\[ G^*(\varphi) = G_c(\varphi) \implies \lambda = \sqrt{\frac{G_c(\varphi)}{G^*(\varphi)}}\]

in the direction that minimizes the load amplitude \(\lambda\)

\[ \varphi = \arg\min_{\varphi' \in [0, 2\pi]} \sqrt{\frac{G_c(\varphi')}{G^*(\varphi')}} \]

Illustration of the GMERR with Wulff plot as proposed by Takei et al. (2013).

where \(G^*\) is obtained from Amestoy & Leblond (1992).

Strong vs Weak anisotropy : \(G_c^{-1} (\varphi)\)

Weak anisotropy

Strong anisotropy

How to parameterize \(G_c(\theta)\) ?

A general parameterization of \(G_c\) can be obtained using Fourier series1. \[ G_c(\varphi) = G_0 \left[ 1 + A_2 \cos(2 (\varphi - \theta_{2})) + ... + A_{2P} \cos(2P (\varphi - \theta_{2P})) \right]. \]

Plots of different \(G_c^{-1}(\phi)\)

\(G_c(\varphi) = 1 + 0.5 \cos(2 (\varphi - \pi/4))\)
\(A_2 = 0.5\)
\(\theta_2 = \pi/4\)

\(G_c(\varphi) = 1 + 0.2 \cos(4 (\varphi - 0))\)
\(A_4 = 0.2\)
\(\theta_4 = 0\)

\(G_c(\varphi) = 1 + 0.8 \cos(4 (\varphi - \pi/6))\)
\(A_4 = 0.8\)
\(\theta_4 = \pi/6\)

Structural tensor: 2D Harmonic decomposition

Blinowski et al. (1996), Desmorat & Desmorat (2015)

The 2P-order model \[ G_c(\varphi) = G_0 \left[ 1 + A_2 \cos(2 (\varphi - \theta_{2})) + ... + A_{2P} \cos(2P (\varphi - \theta_{2P})) \right] \] can be written \[ G_c(\varphi) = G_0 \mathbf{A}_{2P} \bigotimes_{i=1}^{2P} \boldsymbol{n} , \quad \mathbf{A}_{2P} = \mathbf{I}_4 + \mathbf{1}^{\odot 2P-2} \odot \boldsymbol{H}_{2} + ... + \mathbf{1} \odot \boldsymbol{H}_{2P-2} + \mathbf{H}_{2P} \] where

  • \(\mathbf{H}_{n}\) are totally symmetric and traceless
  • \(H_{...00}^{n} = A_{n} \cos(n \theta_{n})\) and \(H_{...01}^{n} = A_{n} \sin(n \theta_{n})\) with \(n=2p\)
  • \(\odot\) is the (totally) symmetrized tensorial product.

Regularization of the fracture problem

Francfort & Marigo (1998), Bourdin et al. (2000)

The state of a domain \(\Omega\) is described by:

  • a displacement field \(\boldsymbol{u}(\boldsymbol{x})\),
  • a crack phase field \(\alpha(\boldsymbol{x})\).

The state fields are governed by an energy minimization problem, \[ (\boldsymbol{u}, \alpha) = \arg\min_{\substack{\boldsymbol{u}' \in \mathcal{U} \\ \alpha' \in \mathcal{A}}} \ \underset{\text{elastic}}{\mathcal{E} (\boldsymbol{u}', \alpha')} + \underset{\text{dissipation}}{\mathcal{D} (\alpha')} - \underset{\text{external work}}{\mathcal{W}_{\mathrm{ext}} (\boldsymbol{u}')} \]

Different strongly anisotropic models

Isotropic fracture model

\[ \mathcal{D}(\alpha) = \frac{G_0}{c_w} \int_\Omega \frac{w(\alpha)}{\ell} + \ell \nabla \alpha \cdot \nabla \alpha \,\mathrm{d}x \]

Strongly anisotropic fracture models

Li & Maurini (2019), Gerasimov & De Lorenzis (2022), Rezaei et al. (2021) (in order)

\[ \begin{split} \mathcal{D}(\alpha) &= \frac{G_0}{c_w} \int_\Omega \frac{w(\alpha)}{\ell} + \ell^3 \nabla^2 \alpha : \mathbf{A} : \nabla^2 \alpha \,\mathrm{d}x \\ \mathcal{D}(\alpha) &= \frac{G_0}{c_w} \int_\Omega \frac{3}{b_w} \frac{w(\alpha)}{\ell} + \ell^3 \nabla \alpha \otimes \nabla \alpha : \mathbf{A} : \nabla \alpha \otimes \nabla \alpha \,\mathrm{d}x \\ \mathcal{D}(\alpha) &= \frac{G_c(\theta)}{c_w} \int_\Omega \frac{w(\alpha)}{\ell} + \ell \nabla \alpha \cdot \nabla \alpha \,\mathrm{d}x, \quad \theta = \arctan \left(- \frac{\nabla \alpha \cdot \boldsymbol{e}_2}{ \nabla \alpha \cdot \boldsymbol{e}_1} \right) - \frac{\pi}{2} \end{split} \]

Other anisotropic models: models with multiple order (Teichtmeister et al., 2017), multi-phase field models (Nguyen et al., 2017), etc.

In practice, it is not that simple …

Using the model of Gerasimov & De Lorenzis (2022) (Foc4)

We observe micro-zigzag on the crack path.

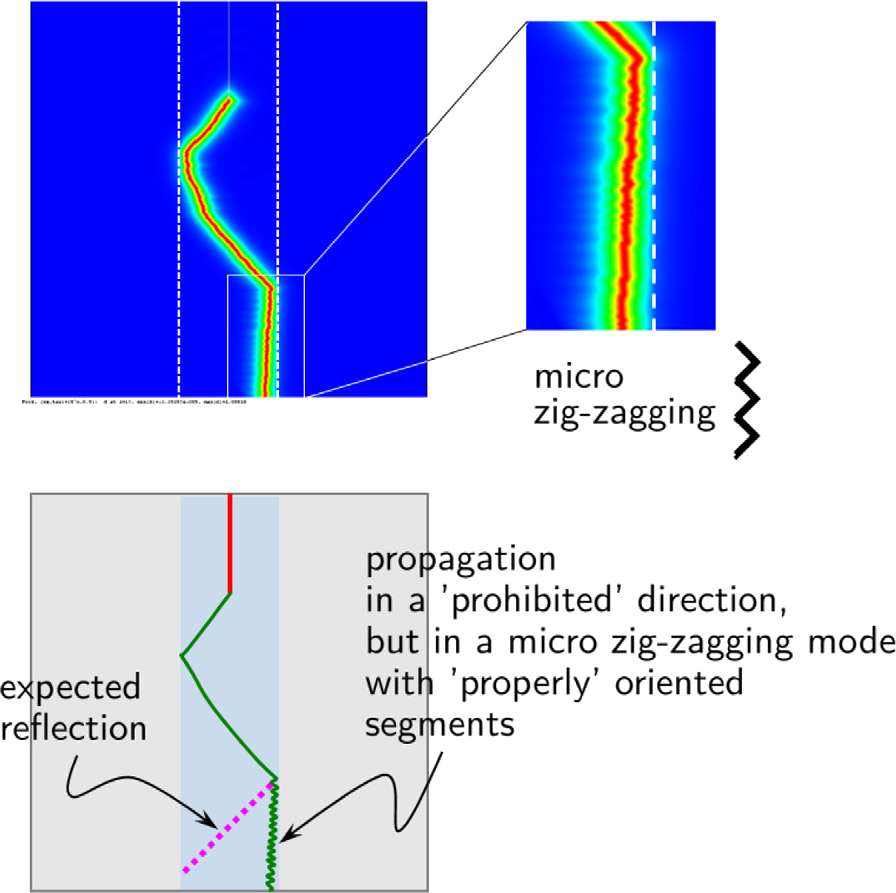Fig. 15 of Gerasimov & De Lorenzis (2022)

… and some more fundamental questions arises

Also discussed by Takei et al. (2013)

The crack propagates when

\[ G^*(\varphi) = G_c(\varphi) \implies \lambda = \sqrt{\frac{G_c(\varphi)}{G^*(\varphi)}}\]

in the direction that minimizes the load amplitude \(\lambda\)

\[ \varphi = \arg\min_{\varphi' \in [0, 2\pi]} \sqrt{\frac{G_c(\varphi')}{G^*(\varphi')}}. \]

Should this minimization be local or global ?

Global vs local minima in the GMERR

Global minimizer

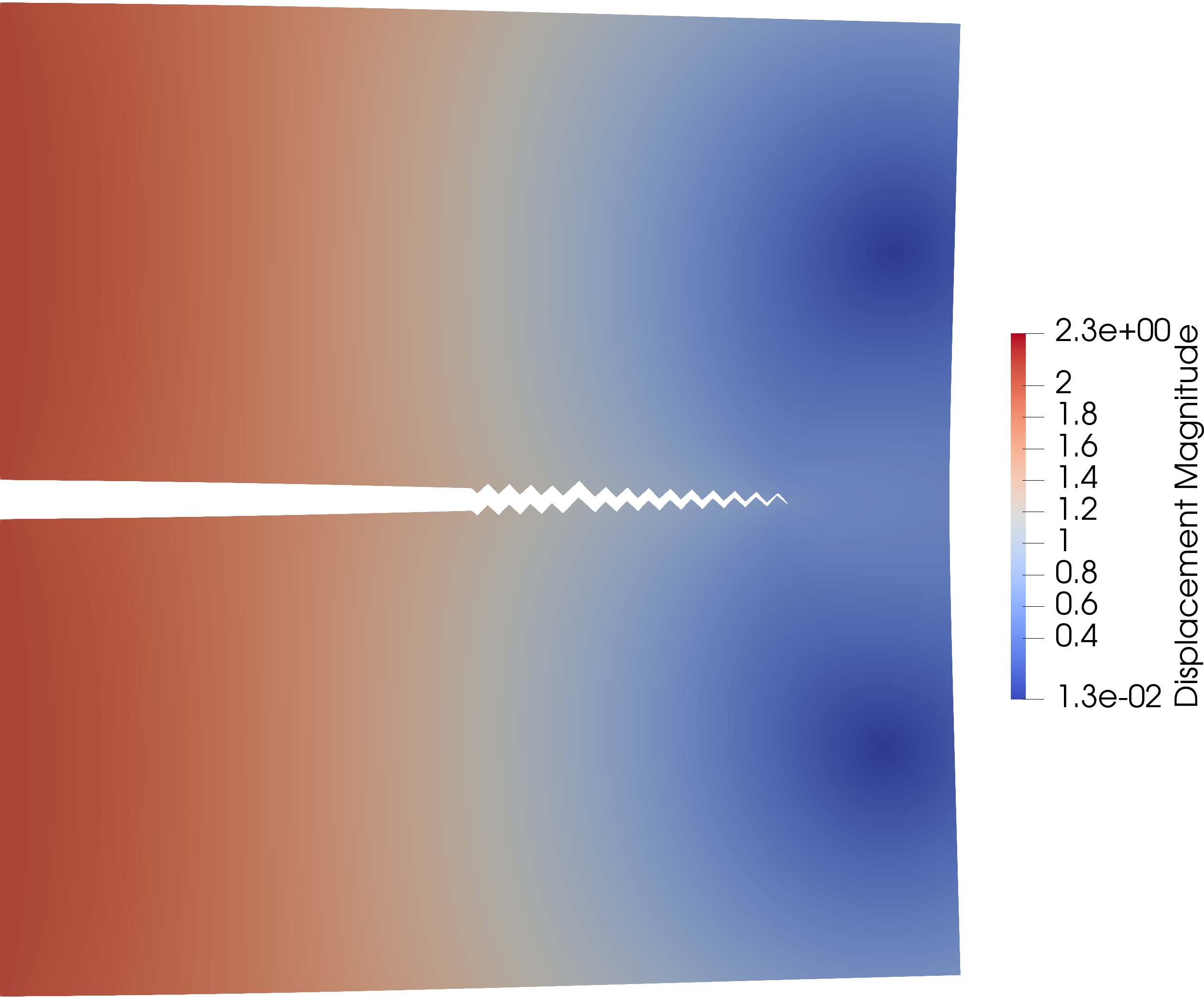
Note: The zig-zag amplitude reduces with crack increment size.

Local minimizer

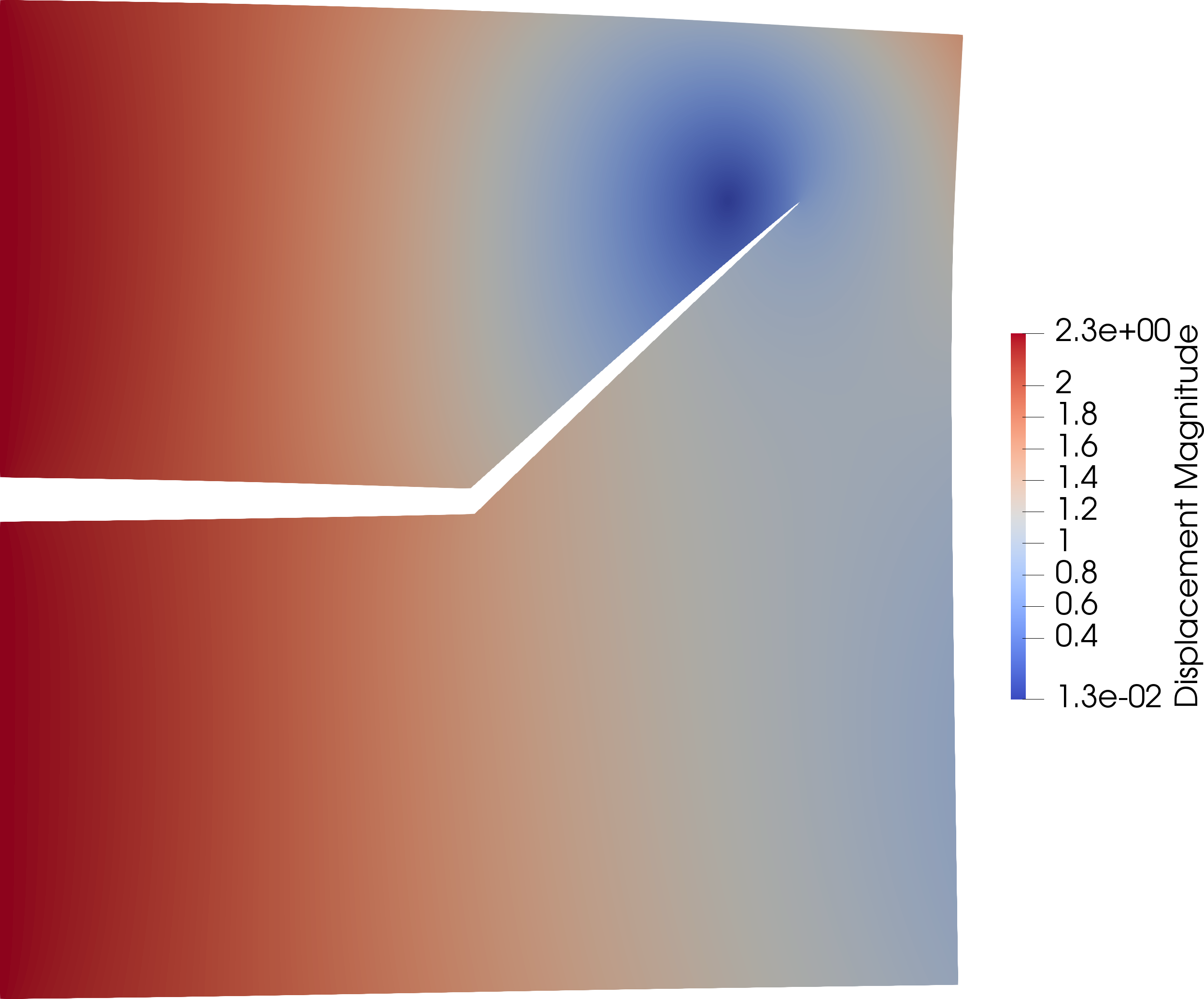
Which solution is correct?

Experiments on strongly anisotropic specimen

PhD thesis of Zhai (2023)

Experiments

Local minimizer

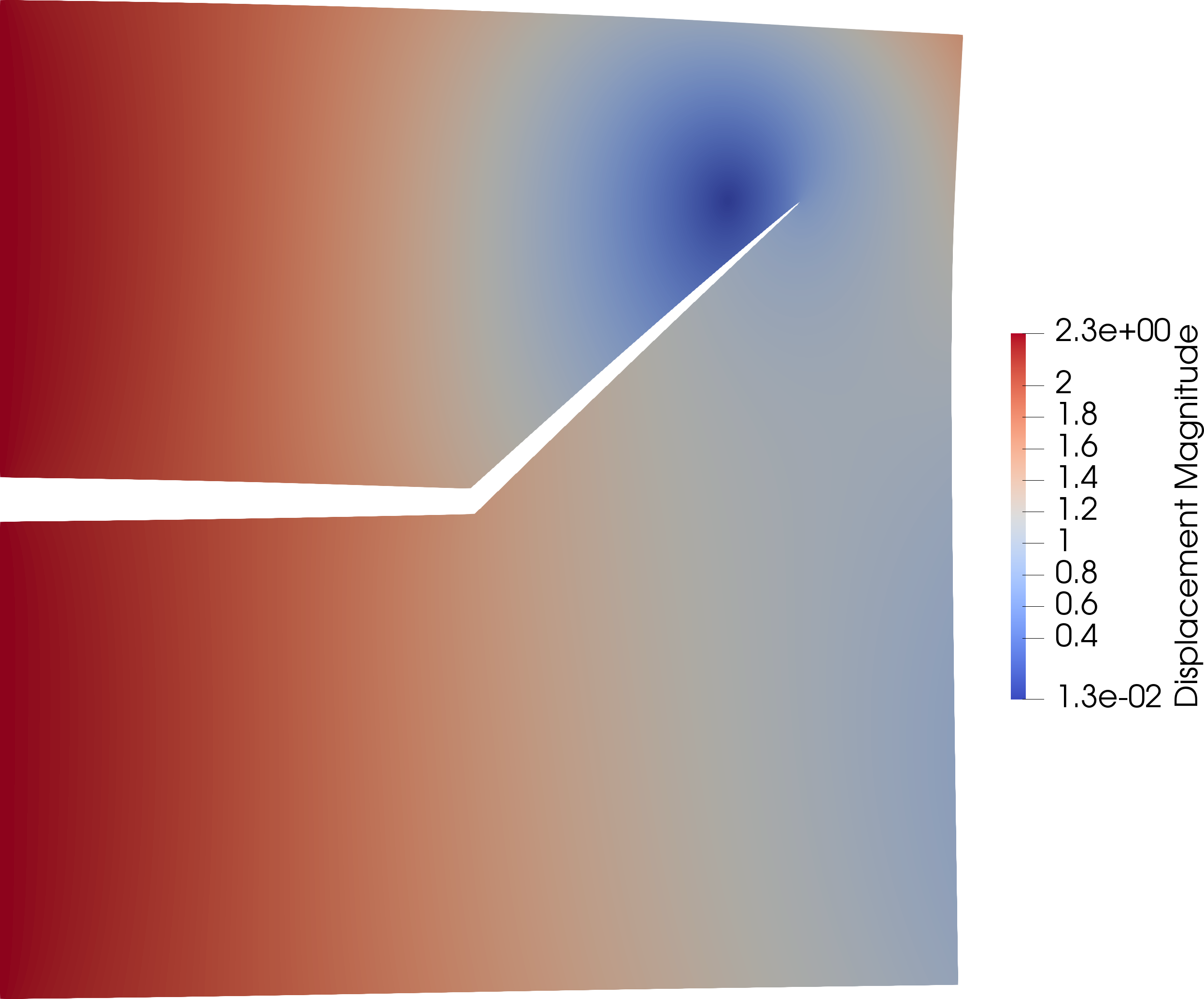
According to those experiments, the local minimizer seems to be valid one.

What about anisotropic phase-field fracture ?

Current partial conclusion


Suggestions

  • Incremental solution of the phase-field problem
  • Use a local minimizer for each load increment for the crack phase.


Load step influence on the crack path
Is there a CFL-like conditions ?
Instable crack propagation
Dynamics (physic solution)
Indirect control1 (quasi-static solution)

Crack propagation in strongly anisotropic media

Using the model of Rezaei et al. (2021)

GMERR

Anisotropic phase-field fracture

Promising first (coarse) results !

Thank you for your attention !

F. Loiseau, V. Lazarus

flavien.loiseau@ensta-paris.fr

Macroscopic bifurcation predicted with the GMERR.

Next objective
More complex fracture case with anisotropic phase-field fracture

References

References

Amestoy, M., & Leblond, J. B. (1992). Crack paths in plane situations—II. Detailed form of the expansion of the stress intensity factors. International Journal of Solids and Structures, 29(4), 465–501. https://doi.org/10.1016/0020-7683(92)90210-K
Blinowski, A., Ostrowska-Maciejewska, J., & Rychlewski, J. (1996). Two-dimensional Hooke’s tensors - isotropic decomposition, effective symmetry criteria. Archives of Mechanics, 48(2), 325–345. https://doi.org/10.24423/aom.1345
Bourdin, B., Francfort, G. A., & Marigo, J.-J. (2000). Numerical experiments in revisited brittle fracture. Journal of the Mechanics and Physics of Solids, 48(4), 797–826. https://doi.org/10.1016/S0022-5096(99)00028-9
Desmorat, B., & Desmorat, R. (2015). Tensorial polar decomposition of 2D fourth-order tensors. Comptes Rendus Mécanique, 343(9), 471–475. https://doi.org/10.1016/j.crme.2015.07.002
Francfort, G. A., & Marigo, J.-J. (1998). Revisiting brittle fracture as an energy minimization problem. Journal of the Mechanics and Physics of Solids, 46(8), 1319–1342. https://doi.org/10.1016/S0022-5096(98)00034-9
Gerasimov, T., & De Lorenzis, L. (2022). Second-order phase-field formulations for anisotropic brittle fracture. Computer Methods in Applied Mechanics and Engineering, 389, 114403. https://doi.org/10.1016/j.cma.2021.114403
Li, B., & Maurini, C. (2019). Crack kinking in a variational phase-field model of brittle fracture with strongly anisotropic surface energy. Journal of the Mechanics and Physics of Solids, 125, 502–522. https://doi.org/10.1016/j.jmps.2019.01.010
Nguyen, T.-T., Réthoré, J., Yvonnet, J., & Baietto, M.-C. (2017). Multi-phase-field modeling of anisotropic crack propagation for polycrystalline materials. Computational Mechanics, 60(2), 289–314. https://doi.org/10.1007/s00466-017-1409-0
Rezaei, S., Mianroodi, J. R., Brepols, T., & Reese, S. (2021). Direction-dependent fracture in solids: Atomistically calibrated phase-field and cohesive zone model. Journal of the Mechanics and Physics of Solids, 147, 104253. https://doi.org/10.1016/j.jmps.2020.104253
Roucou, D., Corre, T., Rolland, G., & Lazarus, V. (2023). Effect of the deposition direction on fracture propagation in a Duplex Stainless Steel manufactured by Directed Energy Deposition. Materials Science and Engineering: A, 878, 145176. https://doi.org/10.1016/j.msea.2023.145176
Takei, A., Roman, B., Bico, J., Hamm, E., & Melo, F. (2013). Forbidden Directions for the Fracture of Thin Anisotropic Sheets: An Analogy with the Wulff Plot. Physical Review Letters, 110(14), 144301. https://doi.org/10.1103/PhysRevLett.110.144301
Teichtmeister, S., Kienle, D., Aldakheel, F., & Keip, M.-A. (2017). Phase field modeling of fracture in anisotropic brittle solids. International Journal of Non-Linear Mechanics, 97, 1–21. https://doi.org/10.1016/j.ijnonlinmec.2017.06.018
Zhai, X. (2023). Crack propagation in elastic media with anisotropic fracture toughness: Experiments and phase-field modeling [PhD thesis].